Comment fait-on un test AB ?¶
- On implémente deux variantes de la même fonctionnalité
- On expose chacune à une partie des visiteurs du site, pendant un certain temps
- On calcule le taux de conversion de chacune des variantes
- On abandonne la moins performante
Un test AB est ...¶
- Une technique de conception de fonctionnalités web / mobile
- Un processus de décision "data-driven"
- Un outil d'optimisation locale de fonctionnalités
Qu'est-ce qu'un taux de conversion ?¶
Si on pouvait exposer la fonctionnalité à TOUS les visiteurs potentiels du site, ce serait le pourcentage de visiteurs qui convertiraient
- Impossible à calculer exactement
- Une propriété fantasmée de la fonctionnalité testée
Que calcule-t-on donc ?¶
- Une estimation du vrai taux de conversion, à partir d'un échantillon
- Si on répète le test avec un autre échantillon :
- On n'aura pas exactement le même résultat !
- On aura, au mieux, à peu près le même résultat
La question maintenant est ...¶
-
Que peut-on dire sur le vrai taux de conversion, à partir de son estimation ?
c'est un job pour ...

La théorie des probabilités, késako ?¶
Description non déterministe du monde.
Si on veut prédire le lancer d'une pièce de monnaie :
- Explication déterministe :
On étudie l'ensemble de lois physiques qui nous diront pourquoi on aura pile ou face.
Explication probabiliste :
Je ne sais pas si je vais avoir pile ou face.
Mais ...
Je sais que si je répète l'expérience assez de fois, j'aurai 50% de piles et 50% de faces.
La théorie des probabilités¶
- Prend en compte notre incertitude: le hasard !
- Décrit les événements par des lois de probabilité
Qu'est-ce qu'une probabilité ?¶
La fréquence d'un résultat, si on pouvait répéter une expérience
"La probabilité d'avoir pile est de 50%"
=
"Si je répète l'expérience assez de fois, j'aurai pile 50% des fois".
Qu'est-ce qu'un taux de conversion ? probabilistiquement parlant...¶
- On a une population ($N$): tous les visiteurs du site LeMonde
- Un nombre de conversions ($X$): partie de la population qui cliquerait sur le bouton, si tout le monde le voyait
- Le vrai taux de conversion: $p = \frac{X}{N}$
Ce vrai taux est impossible à calculer !
Estimer un taux de conversion¶
- On prend un échantillon aléatoire de la population - $n$
- On présente le bouton à cet échantillon, $x$ personnes cliquent
- On calcule une estimation: $\hat p = \frac{x}{n}$
- $\hat p$ est un estimateur de $p$
Nous sommes dans le domaine de l'inférence statistique
Quelques faits de la nature...¶
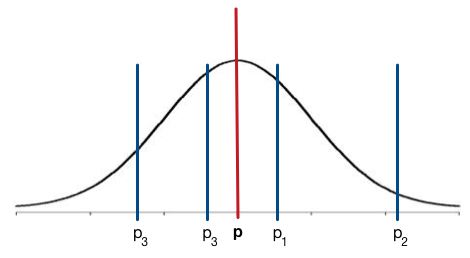
- Si on répète l'expérience, $\hat p$ n'aura pas la même valeur !
- $\hat p$ est centrée autour de $p$
- Elle a un certain "bruit"
Comment la valeur de $\hat p$ varie-t-elle ? Quelle est sa loi de probabilité ?
L'intervalle de confiance
Une fourchette de valeurs "probables" pour $p$, étant donné $\hat p$
Intervalle de confiance à 95%:
$$ p \in \left[\hat p - 1.96 \cdot \sigma_{\hat p}, \hat p + 1.96 \cdot \sigma_{\hat p}\right] $$¶
"Il y a 95% de probabilité que cet intervalle contienne le vrai paramètre p"
Et donc...¶
Au lieu de dire:
"D'après mon test, le taux de conversion du bouton est de 0.02"
On peut maintenant dire:
"D'après mon test, le taux de conversion du bouton est entre 0.01 et 0.03, avec 95% de certitude"
Pourquoi c'est important...¶
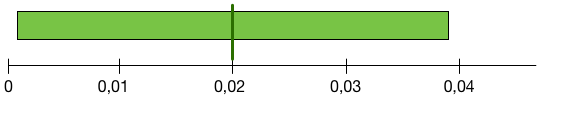
-
$\hat p = 0.02$ et $p \in [0.0002, 0.038]$
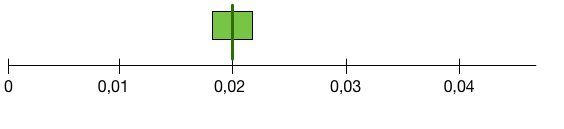
-
$\hat p = 0.02$ et $p \in [0.018, 0.022]$
Un petit exercice...¶
Supposez que vous faîtes un test AB, et vous obtenez le résultat suivant:
- Variante A: $ \hat p_A = 0.2 $
- Variante B: $ \hat p_B = 0.25 $
Quelle variante choisissez-vous ?
Et si vous calculez les intervalles de confiance suivants ?
Variante A: $ \hat p_A = 0.2 $, et $p_A \in [0.01, 0.39]$
Variante B: $ \hat p_B = 0.25 $, et $p_B \in [0.2, 0.3]$
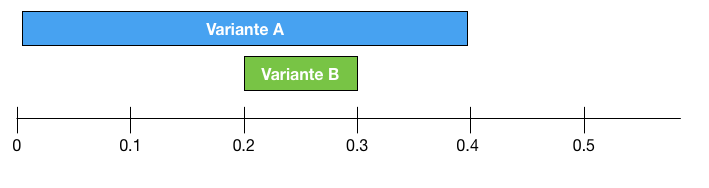
Quelle variante choisissez-vous?
Et maintenant ?
- Variante A: $ \hat p_A = 0.2 $, et $p_A \in [0.18, 0.22]$
- Variante B: $ \hat p_B = 0.25 $, et $p_B \in [0.22, 0.28]$
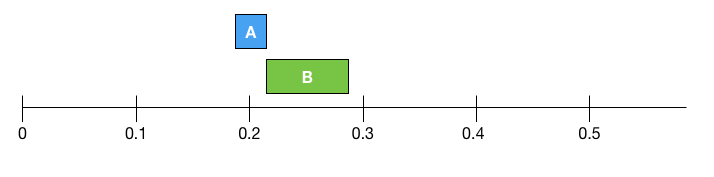
Quelle variante choisissez-vous ?
Avec un peu plus de maths...¶
On peut facilement ajouter de la science à tous nos tests
Quantifier l'(in)certitude de nos décisions¶
- "Je suis sûr à 95% que le taux de conversion est entre 2% et 4%"
- "Je suis sûr à 80% que tel bouton A est meilleur que le B"
- "Je suis sûr à 95% que le bouton C est le meilleur des boutons A,B,C,D,E"
Mieux planifier nos tests:¶
- "Pour choisir entre A et B avec une certitude de 95%, je dois laisser courrir mon test pendant 2 semaines"
Ce qu'il faut retenir¶
- La différence entre un fait et une inférence
- Les décisions projet et les tests AB se basent sur des inférences
- On peut quantifier de degré de certitude des décisions basées sur des inférences
- Une estimation est une fourchette de valeurs, pas une valeur
- Avec un peu de science on peut rendre nos tests plus puissants, et nos décisions plus sûres !
merci